Stock Sequence

The number of up trends of given length in the data set, e.g. there were 1631 days when the stock only went up for one day and then down the next. On the random walk model the up probability is unaffected by the length of sequence, and vice-versa the length of sequence is not affected by any factor other than randomness. The probability of a sequence of two is the probability of a single sequence squared, and so on. The jth root was taken for each percentage where j was the length. The Cum_Root column assumes that the probability of the previous up moves is given by the rows above and so calculated the probability of adding an extra day to the sequence. This is the most important statistic as it shows, on average, the probability of the current (local) up trend from continuing. Obviously the next down may only be a single day before the trend continues. A better analysis is required for what becomes Elliot waves/Fractals etc - to come as soon as I work out how!


Data for FTSE

Length	Count	%	root	cum_root
1	1631	0.484839	0.484839	0.484839
2	853	0.253567	0.503555	0.522992
3	477	0.141795	0.52146	0.559203
4	203	0.060345	0.495633	0.425577
5	109	0.032402	0.503633	0.536946
6	52	0.015458	0.499104	0.477064
7	24	0.007134	0.493556	0.461538
8	9	0.002675	0.476896	0.375
9	2	0.000595	0.438102	0.222222

Data for BP (NYSE)

Length	Count	%	root	cum_root
1	1464	0.462998	0.462998	0.462998
2	783	0.247628	0.497622	0.534836
3	447	0.141366	0.520933	0.570881
4	231	0.073055	0.519891	0.516779
5	103	0.032574	0.504168	0.445887
6	71	0.022454	0.531149	0.68932
7	32	0.01012	0.518832	0.450704
8	19	0.006009	0.527654	0.59375
9	7	0.002214	0.507008	0.368421
10	3	0.000949	0.498558	0.428571

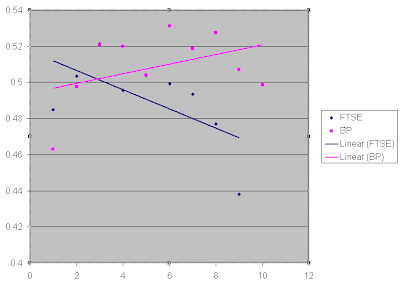The first graph plots the average root, the second graph plots the cumulative root. The data becomes less reliable as the length increases as there are less such events but the general trend seems to be that after ... need to think about this + is it a percentage of the number of sequences, or the percentage of up days in each type of sequence?... think!

Log Actual counts (y) of sequences of up and down of length x from FTSE (1984 to 2010) in blue. The monte-carlo simulation seems to contain an error but is nearly correct.

In a binary sequence a "pair" means 11 following a 0 and preceeding a codon starting in 0. The probability of a 011 sequence is 1/8 and the probabilility that the next codon starts with 0 is 1/2 so 1/16. Thus the probability of sequences of length l is 2^-(l+2)

[check the length of sequences! an error]

Assuming the rare sequences have more error so ignoring the deviance of graph, this suggests that indeed the stock market is random in that ups and downs don't seem to stick together any more than at random.


That said here is a plot of a walk based on the up/down data from the FTSE ignoring the size of the move. It very clearly shows a periodicity in the stock movements. This means the periodicity lies in the up/down data not the distance data. So it is random on the daily level but patterns show up on the macro level.

Finally the need to examine the charts with the extra factor of scale. Not sure yet how to proceed.